Capacitive Circuits

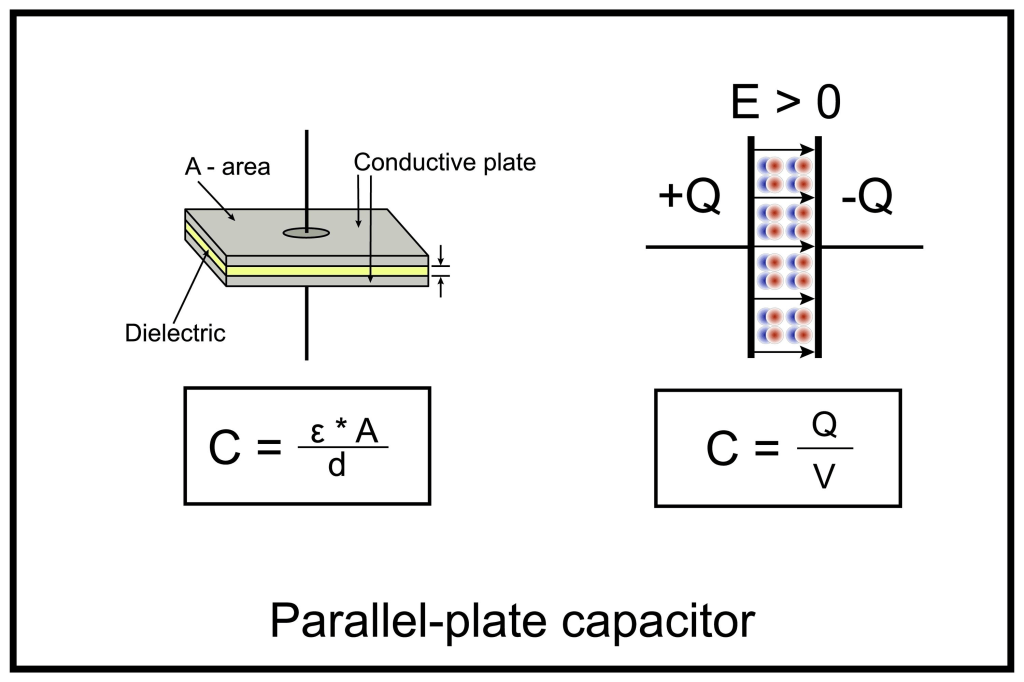
A capacitor is a passive two-terminal electrical component that stores electrical energy in an electric field. It consists of two conducting plates separated by an insulating material known as a dielectric.

Capacitance ( $C$ )

Capacitance is the ability of a body to store an electrical charge. It is defined as the ratio of the change in electric charge ( $Q$ ) to the corresponding change in its electric potential ( $V$ ):

$C = \frac{Q}{V}$

Unit: Farad ( $F$ ). In practice, smaller units are used: $\mu F$ ( $10^{-6}$ ), $nF$ ( $10^{-9}$ ), and $pF$ ($10^{-12}$).
Physical Factors: For a parallel-plate capacitor: $C = \frac{\epsilon A}{d}$ Where $\epsilon$ is the permittivity of the dielectric, $A$ is the area of the plates, and $d$ is the distance between them.

Energy Stored

The energy ( $U$ ) stored in a capacitor is given by:

$U = \frac{1}{2} C V^2$

Capacitor Combinations

Capacitors combine differently than resistors.

\frac{1}{C_{eq}} = \frac{1}{C_1} + \frac{1}{C_2} + \dots + \frac{1}{C_n}

Configuration	Formula	Description
Parallel	$C_{eq} = C_1 + C_2 + \dots + C_n$	Total capacitance increases as plate area effectively increases.
Series	$\frac{1}{C_{eq}} = \frac{1}{C_1} + \frac{1}{C_2} + \dots + \frac{1}{C_n}$	Total capacitance decreases; same charge ( $Q$ ) is on each capacitor.

Capacitors in DC Circuits (Transient Response)

In a DC circuit, a capacitor acts as an open circuit once fully charged (steady state). The process of charging and discharging is called the transient response.

The RC Time Constant ( $\tau$ )

The speed at which a capacitor charges or discharges depends on the resistance ( $R$ ) and capacitance ( $C$ ):

$\tau = R \cdot C$

(Unit: Seconds)

Charging and Discharging Equations

Charging Voltage: $V_c(t) = V_s(1 - e^{-t/\tau})$
Discharging Voltage: $V_c(t) = V_0 e^{-t/\tau}$
Charging Current: $i(t) = \frac{V_s}{R} e^{-t/\tau}$

4. Capacitors in AC Circuits

In AC circuits, capacitors provide an opposition to current flow known as Reactance.

Capacitive Reactance ($X_C$)

Unlike resistance, reactance depends on the frequency ( $f$ ) of the AC signal:

$X_C = \frac{1}{2 \pi f C} = \frac{1}{\omega C}$

High Frequency: $X_C$ is low (capacitor acts like a short circuit).
Low Frequency/DC: $X_C$ is high (capacitor acts like an open circuit).

Phase Relationship

In a purely capacitive AC circuit, the current leads the voltage by 90° ( $\pi/2$ radians). This is often remembered using the mnemonic ICE: I (Current) leads E (Voltage) in a C (Capacitor).

Example Problem: RC Time Constant

Problem: A $10\mu F$ capacitor is connected in series with a $100k\Omega$ resistor to a $10\text{V}$ DC source. Calculate the time constant and the voltage across the capacitor after $1$ second of charging.

Step 1: Calculate the Time Constant ( $\tau$ )

$\tau = R \cdot C = (100 \times 10^3 \Omega) \cdot (10 \times 10^{-6} F) = 1\text{ second}$

Step 2: Calculate Voltage at $t = 1\text{s}$

Using the charging formula:

$V_c(t) = V_s(1 - e^{-t/\tau})$

$V_c(1) = 10(1 - e^{-1/1}) = 10(1 - 0.368) = 6.32\text{V}$

Result: After one time constant ( $1\text{s}$ ), the capacitor is charged to approximately 63.2% of the source voltage.

Summary Table: Resistors vs. Capacitors

Feature	Resistor (R)	Capacitor (C)
Series $R_{eq}$ or $C_{eq}$	$R_1 + R_2$	$\frac{C_1 C_2}{C_1 + C_2}$
Parallel $R_{eq}$ or $C_{eq}$	$\frac{R_1 R_2}{R_1 + R_2}$	$C_1 + C_2$
DC Behavior	Dissipates energy	Blocks DC (Steady state)
AC Behavior	Voltage/Current in phase	Current leads by 90°